Difference between revisions of "Rendezvous"
m (HasPrecis test) |
(→Rendezvous burn: Grammar) |
||
| Line 43: | Line 43: | ||
If the time to rendezvous is shorter than one [[orbital period]], its possible to ignore most orbital mechanics and instead assume both craft are in a gravity-free space. That concept gets used very often in various [[radar]] rendezvous guidance systems ([[Gemini]], [[Soyuz]]). Instead of making orbital maneuvers, which would need fast computers to calculate, the chasing spacecraft uses a [[Doppler effect|doppler radar]] to measure the angle, distance and rate of change of the distance. By keeping the angle between [[line of sight]] to the target (measured by the radar) and its own velocity vector constant ([[proportional guidance]]), the chasing spacecraft approaches the target very effectivly. | If the time to rendezvous is shorter than one [[orbital period]], its possible to ignore most orbital mechanics and instead assume both craft are in a gravity-free space. That concept gets used very often in various [[radar]] rendezvous guidance systems ([[Gemini]], [[Soyuz]]). Instead of making orbital maneuvers, which would need fast computers to calculate, the chasing spacecraft uses a [[Doppler effect|doppler radar]] to measure the angle, distance and rate of change of the distance. By keeping the angle between [[line of sight]] to the target (measured by the radar) and its own velocity vector constant ([[proportional guidance]]), the chasing spacecraft approaches the target very effectivly. | ||
| − | When better computers are available, its also possible to solve [[Hills equations]], which describe the movement of an object relative to another in an orbit. | + | When better computers are available, its also possible to solve [[Hills equations]], which describe the movement of an object relative to another in an orbit. This is more effective in terms of fuel and more accurate, but requires better onboard computers, as it requires solving differential equations. |
===Rendezvous=== | ===Rendezvous=== | ||
Revision as of 11:52, 1 October 2009
In spaceflight, rendezvous refers to the event in which two spacecraft meet. This does not neccessarily occur in space: a rendezvous can also happen on the surface of a celestial body.
In orbit
A rendezvous usually takes place in orbit, e.g. when spacecrafts are travelling to a space station. If two spacecraft are close enough to each other (< 300m) and travel in similar orbits they are said to rendezvous. In such a situation, both spacecraft can stay close to the space station with minimal corrections (linear RCS).
There are two ways to bring about rendezvous:
- direct insertion into the space station's orbit, or
- insertion into a catch-up orbit.
A direct insertion needs more propellant and allows only few windows for insertion. If launching from the surface, the spacecraft not only has to align its orbital plane with that of the other spacecraft, but also to do its final insertion burn close to the space station. Because of the very rare launch windows and high propellant demands the alternative way — inserting the spacecraft into a catch-up orbit — is preferred.
Catch-up orbit
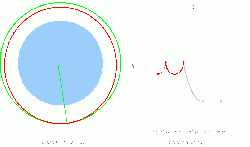
The best launch window for a catch-up orbit is one that places the ship into the same orbital plane as the target but with a significantly lower orbit. The important measure is the difference between the semi-major axis, since the semi-major axis defines the time needed for one revolution around Earth.
The point at which the spacecraft should leave the (almost circular) catch-up orbit can be calculated using this formula:
where
- - the distance angle between the chasing spacecraft and the target spacecraft.
- - the number of apogee passes on the transfer ellipse.
- - the semi-major axis of the transfer ellipse.
- - the radius of the target orbit (assumed circular).
When this angle is reached, the chasing spacecraft performs a prograde burn to enter the planned transfer ellipse. This is called the intercept burn.
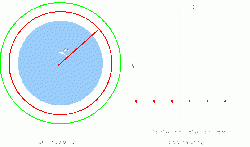
Rendezvous burn
When reaching the final apogee pass of the transfer ellipse, all possible errors will usually bring the spacecraft away from its desired course (including errors because the initial orbits have not been perfectly circular). Because of that influences, the next orbit is usually not the final target orbit, but again a less eccentric chasing orbit. The parameters of this orbit can be calculated using the following formula:
- The spacecraft arrives at the target point before the target:
- The target arrives at the target point before the chasing spacecraft:
The variable again describes, how many orbits the chasing craft should wait in the immediate orbit until it meets the target.
If the time to rendezvous is shorter than one orbital period, its possible to ignore most orbital mechanics and instead assume both craft are in a gravity-free space. That concept gets used very often in various radar rendezvous guidance systems (Gemini, Soyuz). Instead of making orbital maneuvers, which would need fast computers to calculate, the chasing spacecraft uses a doppler radar to measure the angle, distance and rate of change of the distance. By keeping the angle between line of sight to the target (measured by the radar) and its own velocity vector constant (proportional guidance), the chasing spacecraft approaches the target very effectivly.
When better computers are available, its also possible to solve Hills equations, which describe the movement of an object relative to another in an orbit. This is more effective in terms of fuel and more accurate, but requires better onboard computers, as it requires solving differential equations.
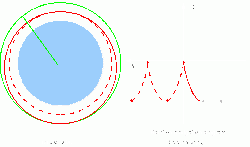
Rendezvous
When the target is reached, the orbital parameters of both craft should be equal. At close distances, its enough to just neutralize any velocity difference.
On the surface
Rendezvous on the surface of a planet is not nearly as difficult as in orbit since the speeds involved are much smaller. The presence of an atmosphere also simplifies maneuvers for aerodynamic vessels. The simplest way to perform a surface rendezvous is to fly directly towards the other spacecraft.
When the other spacecraft is far away (such as on the other side of the planet), a more fuel-efficient way to get there may be via a ballistic trajectory. This can be thought of as "throwing" the spacecraft towards the target, and letting it fall close to it. On planets with no atmosphere the Map MFD can be used to estimate and adjust the ballistic trajectory and the landing point.
The first and so far only historic example of a surface rendezvous was the landing of Apollo 12, where its LM landed only about 200 m away from its target, the lunar probe Surveyor 3.
Another kind of "surface rendezvous" happened in August 1990 in the Kennedy Space Center. When the space shuttle Atlantis (STS-43) rolled back from pad 39 to the VAB for repairs, after a fuel leak and hail damage, it passed close to the space shuttle Discovery (STS-41), which headed for the same pad for its scheduled launch.
See also
- Rendezvous MFD, an Orbiter implementation of Hills equations in a MFD.
- STS guidance MFD and Soyuz guidance MFD, two similar MFDs which implement automatic rendezvous and station keeping.
Precis
This article has a precis and appears in the Random addon or Random article section on the Main Page. The precis can be found at Rendezvous/precis and is displayed below.
|
In spaceflight, rendezvous refers to the event in which two spacecraft meet. This can occur in space or on the surface of a celestial body. A rendezvous usually takes place in orbit, e.g. when spacecrafts are travelling to a space station. If two spacecraft are close enough to each other (< 300m) and travel in similar orbits they are said to rendezvous. In such a situation, both spacecraft can stay close to the space station with minimal corrections. (More...)
|
![{\displaystyle \Delta \varphi =\pi \left[1-(2m-1)\left({\frac {a}{r_{z}}}\right)^{\frac {3}{2}}\right]}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/58602fb405f4094ed711d3bdfb0be04fbab588f3)