Difference between revisions of "GPIS 10: I Was Just Wondering"
(Original from GPIS 3rd edition) |
(set up for random page) |
||
| Line 213: | Line 213: | ||
|style="text-align:right" width="33%" |[[GPIS_Epilog|Epilog: Your Future In Space]] | |style="text-align:right" width="33%" |[[GPIS_Epilog|Epilog: Your Future In Space]] | ||
|} | |} | ||
| + | |||
| + | [[Category:Tutorials]] | ||
| + | {{HasPrecis}} | ||
Revision as of 23:32, 7 March 2015
| Chapter 9: A Bit About Add-ons | GPIS Contents | Epilog: Your Future In Space |
Acknowledgement
This material was originally contributed by Bruce Irving from the 2nd edition of Go Play In Space, where it was chapter 9. Refer to the page's View History tab to see subsequent changes.
I Was Just Wondering...
We all wonder about things, and with the abundance of information on the web, and with the availability of powerful and easy to use search engines like Google, anyone with an Internet connection needn’t wonder for long. And yet... sometimes it’s hard to find just the right question to get just the right answer for some special topic where you know more than the average “civilian” yet you really aren’t an expert either. Sometimes there’s too much information to sort through even with Google’s help. When you find 7,437 needles in the haystack (in 0.07 seconds), which is the right needle?
I can’t solve this problem in general, of course, but even after pointing you toward the books and web sites in chapter 5, I don’t want to just say “you can find that for yourself on the web” for everything (though you probably can). I think I may know a few of the things you might be wondering about when it comes to space and Orbiter, because I was wondering about some of them myself not too long ago. So here are a few to get you started, with pointers to the web to help you get farther along. Note that this information is all optional! You don’t need to know the information in this chapter to have fun and success with Orbiter!

You may consider this to be a pretty unusual selection of questions, since it does not include many that might truly be “frequently asked,” such as “how do I install add-ons?” Aside from the fact that I’ve covered a number of such topics elsewhere in this book, I’m also not really trying to make a general purpose FAQ here. It’s really more along the lines of “I wanted to discuss this but didn’t want to clutter the main text any more than it already was!” There are some real Orbiter FAQ’s on the web. Here are a few I have found (the usual disclaimer about web sites moving applies here – I actually found these just now by searching google.com for orbiter simulator FAQ).
http://www.medphys.ucl.ac.uk/~martins/orbit/faq.html (official FAQ, mainly troubleshooting)
http://orbit.m6.net/v2/read.asp?id=24924 (“sticky” topic for FAQ on the main Orbiter Web Forum)
http://www.eharm.net/shop/freeware/orbiter/orbiter_faq/orbiter_faq.html
Questions About Orbits and Zero-G
What is up with this orbit thing? And what about zero-G?
I’ve heard a lot of questions about orbits and about zero-G – and it turns out these are closely related. Here are a couple of more detailed variations that I was once asked by a Ph.D. in the life sciences:
This orbit thing bothers me – a spacecraft can circle the Earth for years at high speed without requiring power or slowing down? How does that work? And what about zero-G, is there really no gravity above some height like 300 km?
You can probably find dozens of answers to these questions on the web, and I will give it a shot too (the short answer: it’s all just a really, really long fall). But instead of starting with the usual “cannon ball firing from a tall mountain” example, let’s start with something you have actually experienced – throwing a ball. In this case, your arm provides the “thrust” (force) that accelerates the ball from zero speed (in your hand) to some final speed (40 m/s or even faster for a major league baseball pitcher, much slower for most people). If you throw a ball level (parallel to the ground), you are giving it a lot of horizontal velocity (HVEL). If you throw it straight up, it’s mostly vertical velocity (VVEL). In either case, air drag slows it down, and gravity pulls it back to Earth in a few seconds. You probably know that if you throw it harder (faster initial speed), it will go a longer horizontal distance, or it will rise higher, or some combination (let’s ignore cases like paper airplanes – these can generate lift from moving through the air, which is a force that opposes gravity and lets it stay up longer).
So NOW we will drag that old cannon up to the top of a really, really tall mountain that doesn’t actually exist. Why? Because not even professional baseball pitchers can throw things fast enough, and by getting on a really big mountain, we imagine getting above most of the atmosphere so there’s little air drag on the (cannon) ball. In this “thought experiment,” we aim the cannon horizontally (level with the ground), and the throwing force comes from an explosion inside the cannon. The cannon is fired and the cannonball’s path starts out horizontal but is pulled down by gravity, creating a curved path (it’s actually pulled toward the center of the Earth, but for a short distance, this is close enough to “down”). With a small explosion, the cannonball travels a few kilometers before hitting. It’s clear that it is falling toward the Earth and that its horizontal velocity (HVEL) has just carried it some distance from the mountain before gravity pulls it down. In this short distance, the Earth hasn’t “curved away” very much, and the time to hit the Earth is almost the same as if we just dropped it straight down from the mountain (if the Earth were flat and had no air, it would be exactly the same time to reach the ground, dropping or throwing level).
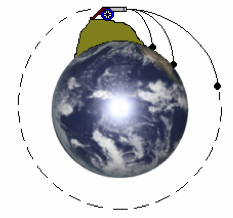
But the Earth is actually round, and let’s say we get a really huge cannon that can make a huge explosion without disintegrating and we get that cannonball going at around 8000 m/s. What would happen then? Gravity would still pull the ball (let’s forget the cannon part now) toward center of the Earth, creating a curved path as before. But traveling so fast, the ball goes several meters of “horizontal” distance for each meter of vertical distance that it falls. And the strange thing is, since the Earth is of course not flat, but “curves down” at about the same rate as the ball curves down, the falling ball doesn’t hit the surface yet...
So what happens? The ball just keeps falling, but it never hits the Earth’s surface! The “curving down” of the Earth’s round surface means that the ball keeps falling, but sort of “down and around” the Earth. Theballisinorbit! That’swhyit’scorrecttosaythatanorbitisjustareally,reallylongfall.Gravityhas definitely NOT gone away – it is steadily pulling the ball toward the Earth’s center. But the Earth’s surface “curves down” faster than the ball falls down, and the ball never hits (unless air drag or something else “wears down” its orbit – remember this is just a thought experiment, but it’s basically right).
But what about the zero-G thing? We’re finally there! The key to THAT is the very same idea of falling. If you are in a spacecraft in orbit, you are in “free fall” and without the surface of the Earth to push back on you, or anything to slow you down, you feel no forces on your body, not even your weight (weight is actually a force, the force you feel normally just standing on Earth when gravity pulls you down against the ground or floor – you really feel the ground or your chair “pushing up” against your body). You feel no weight, so you are “weightless.” Zero-G doesn’t mean gravity has gone away or become zero. Gravity is still very much in the picture, pulling your spacecraft down and around the Earth.
So how are orbits defined, and how do I interpret all those numbers that Orbiter displays?
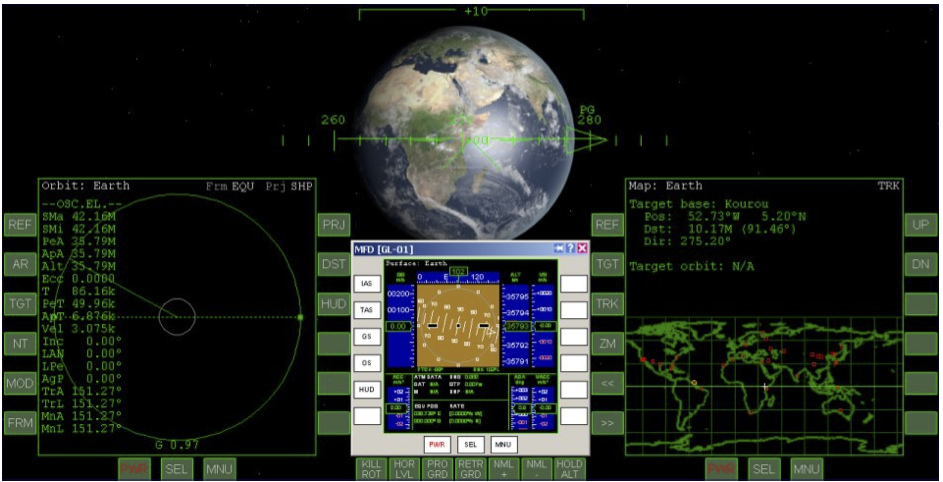
Orbits are defined by orbital elements, and these are displayed on the Orbit MFD. The Orbit MFD buttons, abbreviations, and screen symbols are pictured and defined in section 13.2 (pages 50-52), and the orbital elements themselves are defined in mathematical detail in Appendix C (pages 109-110). Orbital elements are the numbers that define the an orbit in detail, and these are shown in several forms in the Orbit MFD. There are only 6 elements required to define an orbit, but the data can be expressed in several forms for convenience depending on what you want to do. The Orbit MFD actually shows 18 values. Here are some pictures which may clear things up a bit.
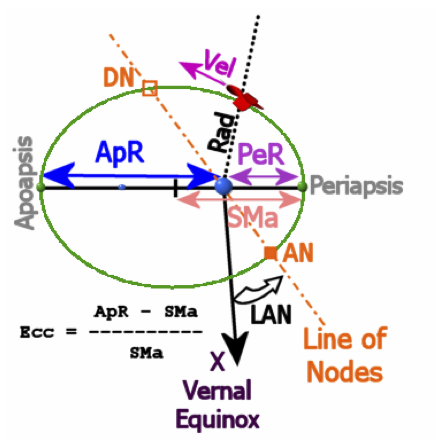
Inclination (Inc) defines the “tilt” of the orbit with respect to the equator, in degrees, and period (T) is the amountoftimeinsecondstocompleteoneorbit. Therestofthelistedelementsarealsomeasuredin degrees, but they represent angular measures for various positions in the orbit, generally defined as “longitude” from a reference direction. I will give LAN (longitude of the ascending node) as an example and refer you to the Orbiter manual for the others.
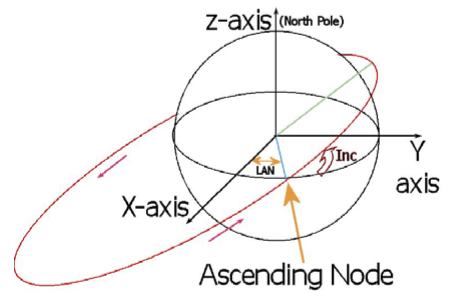
Why is LAN important? You can perhaps see from the picture above that even if you change only the LAN for an orbit, the orbit will point to a different direction in space. So even if the sizes and shapes of two orbits are the same (apoapsis, periapsis, eccentricity), and even if their inclinations to the equator are the same, if the LAN is different, each will visit a different region in space.
For more information on orbital elements, I recommend the following web sites: http://spaceflight.nasa.gov/realdata/elements/index.html http://en.wikipedia.org/wiki/Orbital_element
| Point of Confusion – What is “longitude?”
In common use, longitude refers to an east-west position on the surface of the Earth, used along with latitude for north-south position. We also use the term “longitude” in talking about orbits, but it’s a different thing, not this surface-based longitude (referring orbital information to surface locations would beabitofaproblemsincetheEarthrotatesevery24hours). Longitudeinorbitaltermsisstillasort-of east-west measure, but it refers to a fixed direction in space. Fixed how? Keep in mind that in addition to the Earth’s daily rotation, the Earth travels around the Sun every 365 or so days. So we need to do something to define a coordinate system for orbital elements that stays (nearly) fixed (at least fixed for a long time, some years). This can be done by using the direction to a distant star as the reference direction (this does require adjustment every few years since even the stars are not exactly fixed relative to our Sun). The direction of the Vernal Equinox (spring position of the Sun with respect to the stars) in a certain year (2000 in Orbiter) is used as this reference direction. |
What is a geostationary orbit?
A geosynchronous orbit is one whose orbital period matches the rotational period of the Earth (about 23 hours, 56 minutes or 86,164 seconds) . If the orbit also has zero inclination (i.e., it orbits directly above the equator), then the satellite will appear to hang stationary over one point on Earth, and it can also be called geostationary. Such an orbit is very useful for communication satellites. Current piloted spacecraft don’t go anywhere near this height, but future space stations may also find these positions useful.
Orbiter includes a scenario that demonstrates a geostationary orbit, with a Delta Glider orbiting above a point in East Africa as shown above. This scenario is found in the folder Special orbits, which is inside the Navigation folder. Notice some interesting things about the above screen shot (an External MFD has been added to show the Surface MFD). The altitude is 35,790 km (22,400 miles), inclination and eccentricity are zero, period (T) is 86.16k seconds. The map shows the constant position above Africa, and the ground speed (GS) shown in the Surface MFD is 0.00 m/s. That’s geostationary!
General Space Flight Questions
Why do most rockets have more than one stage?
This is due to a combination of necessity and efficiency. Most of the mass of any current technology rocket is fuel, and there also must be some structure and mechanism to make use of the fuel (fuel tanks, pipes, pumps, etc.) in addition to the rocket engines and the payload. As fuel is used up, weight is reduced, but it can be reduced even more by getting rid of any structures and mechanisms that are no longer needed. One way to do this is with stages – when the fuel for the first stage is exhausted, the entire stage is ejected, and the second stage engines can now be used more efficiently since they do not have to accelerate the unneeded mass of the discarded first stage.
There are variations on this, such as the Space Shuttle’s use of two solid rocket boosters (SRB) that are “strapped on” and burn to provide a lot of additional thrust for the first 2 minutes of flight, along with the Space Shuttle Main Engines (SSME) that burn liquid fuel and oxidizer from the external tank. At 2 minutes, the SRB fuel is exhausted and the SRB canisters are dropped (parachutes allow them to be recovered at sea for refurbishment and reuse). The SSME’s continue to burn, accelerating the now lighter Orbiter vehicle and external tank to orbit. This is sometimes called a “zero stage” method.
There are disadvantages in terms of complexity and costs of multi-stage rockets, but until advanced materials, propellants, and engines are developed that allow “single stage to orbit,” variations of the multi- stage approach will continue to be used. This could include aircraft-type first stages such as the hypothetical “TX” shown in chapter 8. See http://en.wikipedia.org/wiki/Staging_%28rocketry%29 .
How does a real spacecraft know how fast it’s going and where it is?
There are several ways that are used to keep track of the position, speed, and acceleration of spacecraft. One method is called an inertial navigation system (INS). In an INS, gyroscopes are used to keep track of the (x, y, z) directions in 3D space relative (say) to the stars, even as the spacecraft moves and rotates. Special sensors called accelerometers can continuously monitor any accelerations in each direction (from gravity, engines, thrusters, air drag while in the atmosphere, etc.). Since acceleration is defined as a change in velocity (speed and direction), and velocity is defined as a change in position, computers can use this constantly updating information to keep track of the acceleration, velocity, and position in real time.
For more details, see http://en.wikipedia.org/wiki/Inertial_navigation_system . By the way, Orbiter does much the same thing as this, but for Orbiter, the calculations are done many times a second to actually determine your simulated acceleration, velocity, and position as you fire thrusters or engines (thrust forces), fly through the atmosphere generating lift (aerodynamic forces), or get closer or farther from large bodies such as the Sun, planets, and moons (gravitational forces).
In addition to the INS, spacecraft near the Earth (or even quite far from Earth, even near Mars or Jupiter) are tracked by Earth-based radar systems. These systems send out high-power radio waves which reflect from the spacecraft. The reflected signal may be very faint, but they can still measure its direction, how long it took to get back, and any change in its frequency. From this information, they can accurately calculate the spacecraft’s position and velocity. They can also do similar things with a radio signal that can be sent by the spacecraft (from a transponder or communication radio).
What is “Delta-V” and why is it important?
Delta-V (ΔV) is an abbreviation for “delta velocity.” The Greek character delta (Δ) is used in mathematics to represent the change of some quantity, so delta-V means “change in velocity.” Since velocity is directly related to energy (specifically kinetic energy), and a certain amount of energy is required to move from one state (a particular position and velocity) to another, delta-V is very useful in the planning of space missions. This is because each type of flight (e.g., Earth surface to low Earth orbit [LEO], LEO to the Moon, LEO to Mars, etc.) has a characteristic delta-V associated with it. Although the delta-V can vary somewhat depending on the dates and on the exact route taken, there is always a minimum delta-V for any direct flight, and if you know the available delta-V from your launch vehicle and spacecraft, this establishes whether a particular mission is possible. Here are typical delta-V values for some flights.
| Starting point | End point | Delta-V (meters/second) |
|---|---|---|
| Earth surface | Low Earth Orbit (LEO) | 9,300-10,000 |
| LEO | Low Lunar Orbit (LLO) | 4,200 * |
| LEO | Lunar Surface | 6,300 |
| LLO | Lunar Surface | 2,000 |
| LEO | Trans-Mars Injection (TMI) | 3,600 |
| TMI | Mars Orbit (300 km circ.) | 2,400 |
| Mars Surface | Low Mars Orbit (LMO) | 4,100 |
| LEO | Ceres (central asteroid belt) | 8,600 |
* includes delta-V for both Earth orbit eject and lunar orbit entry braking
What is “available delta-V?”
This depends on the thrust of the engines, the amount of fuel carried, and the payload to be carried. For a given amount of thrust and fuel, you can give a small payload more delta- V than a large payload. This is why many satellites can be launched to orbit or even to the Moon or Mars with relatively small rocket boosters – unpiloted satellites can be made pretty small these days. There are equations for all this (the basic one is often called “the rocket equation,” see references below) and they can be worked “backwards,” meaning you start with the payload you want, say “100 metric tons on Mars” and from that you can figure out how much thrust and fuel you need to achieve the delta-V to reach Mars (probably concluding you don’t have a big enough booster to achieve that mission yet). Or you can say “how much mass can we get to Mars with available boosters?”
For reference purposes, the Space Shuttle Main Engines (SSME) and the Solid Rocket Boosters (SRB) provide very close to the delta-V needed to reach a circular low Earth orbit (LEO) of about 400 km altitude (about 9700 m/s – note that this is more than the speed you will have in the Orbit MFD, around 7800 m/s, because it includes the delta-V needed to overcome atmospheric drag). Once it is in orbit, the OMS engines (Orbital Maneuvering System) can provide the Shuttle with about 1300 m/s of additional delta-V for orbit changes (rendezvous with ISS, reentry burn, etc.). The (hypothetical and futuristic) Delta Glider, in contrast, has a very high main engine exhaust velocity (40,000 m/s – this seems to suggest a gas- core nuclear fission engine, and there’s a hint of this in the yellow radiation warning symbols above the main engines, but the details of engines are not modeled anyway, only their performance). With this exhaust velocity and with only 58% of its mass as fuel, its available delta-V is about 36,000 m/s.
You can’t fool Mother Nature when it comes to energy, but there are some “tricks.” The basic trick is multiple stages – throw away mass you don’t need (e.g., the empty first stage), giving a lower remaining mass that you can accelerate to a higher velocity. Another “trick” is gravitational assist – instead of going directly to the target planet, you calculate a path to pass close to another planet (without orbiting or hitting it) in a way that uses its gravity to speed up the craft and send it in the right direction for the target planet (sometimes called a “slingshot maneuver”). Venus can be used this way for Mars flights (for example).
For more on delta-V, see http://en.wikipedia.org/wiki/Delta-V and http://en.wikipedia.org/wiki/Delta- v_budget and the various links on those pages. There is also a very good web page on delta-V and rocketry here: http://www.pma.caltech.edu/~chirata/deltav.html (with a useful graph that relates fuel fraction, exhaust velocity, and delta-V, which I used in the Delta Glider estimates above).
Another great resource for interplanetary and lunar flight planning is the personal web site of Dr. Donald Rapp, http://www.mars-lunar.net/ and in particular for this question, his paper on the rocket equation and specific impulse (this three-page, 107 kB PDF file also includes a more extensive table of delta-V values for various flights): http://www.mars-lunar.net/Arch.Elements/1.Rocket.Equation.pdf. There are many other PDF files on trajectories and other technical planning issues, primarily for Moon and Mars missions. Dr. Rapp has extensive practical experience in space mission planning at JPL.
What about the risks of human space flight?
Every human activity has some risk – you could even get hurt climbing out of bed. But some things are clearly more risky than others, and many people think that flying in general, and space flight in particular, is especially risky. It is true that spacecraft use explosive fuels, fly very fast and high, and go where there is not enough air for humans to survive unprotected. These things can be dangerous if not handled carefully and correctly, but this is why space flight requires special hardware and software systems, extensive testing of the systems and procedures, and very intense training and practice for all the people involved. Even with these efforts, problems can occur, and in a few cases, the problems can be bad enough to kill people, as we know from the losses of Space Shuttles Challenger (1986) and Columbia (2003).
But consider that early airplanes were also very risky, and that when airline travel started in the 1930’s, there were many crashes. Some people wanted the speed and convenience (and adventure, at that time) of flying – they were willing to take the risk even though the systems and procedures still had many problems. A lot of advanced technology was developed for World War II (things like radar and jet engines that allow planes to fly very high, above most of the bad weather), and since then (with many more developments), airline flying has become so safe that almost everyone trusts it. Of course there are still airplane crashes, but they are so unusual that each one is considered major news (unlike car crashes, which kill many people every day and are only local news if that).
Piloted space flight is still in its early stages – it is experimental flight, not routine flight. NASA and other space agencies work hard to make it as safe as possible, but it is not perfectly safe, and astronauts understand this. They choose to do it because they feel it is important (and for the adventure and other reasons too). Many people accept risky jobs such as high rise building construction because they need the work, and perhaps also enjoy it as a challenge. Other people enjoy risky hobbies such as mountain climbing. As space flight becomes more common, it will also become safer. There will also be more benefits from space flight over time, some of them not fully known yet. Many people (including me) believe that the known and potential benefits justify the risks of space flight. But there definitely are risks. For information on space disasters, see http://en.wikipedia.org/wiki/List_of_space_disasters
Questions About Orbiter
Why are you teaching space flight in a fictional rocket plane instead of in the Space Shuttle or Apollo or something else that’s real?
You may know from chapter 9 that Orbiter allows you to install and fly add-ons for all sorts of realistic spacecraft, from historic unpiloted satellites and probes to Mercury, Gemini, Apollo, and the Space Shuttle (and even more when you consider available Russian spacecraft). “Realistic” is cool, but it is also limiting. These are all “early” spacecraft, though based on technology that was the best in the world at the time they were designed (even the Shuttle is “early” – it was designed in the 1970’s). They typically have just enough fuel and payload to fly their specialized missions, and not much more (even the general-purpose Shuttle has a pretty narrow mission, “fly a cargo to low Earth orbit”). With weaker engines, they typically need multiple stages (see General Space Flight Questions), which makes them more complicated and expensive to operate.
To do much better than this requires advanced materials (super strong but light weight and heat resistant) and advanced engines that can provide more thrust for longer periods with less fuel. Such things are not prohibited by the laws of physics – they are under development but don’t exist yet, except in the form of “fictionalbutphysicallyrealistic”simulatedcraftsuchastheDeltaGlider. Suchcrafthavebeenstudied under the name “single stage to orbit” (SSTO), and we will have them eventually. In the meantime, they are simpler to operate in Orbiter, and they still teach you all the right stuff.
Isn’t it cheating to use slowed-down time?
First of all, what is “cheating” in a single player simulation game anyway? The main goal of Orbiter is to provide a way to learn something about space flight in a realistic but fun way. One of the attributes of space flight is that some events happen very fast or require precision timing (like turning on a rocket engine for a maneuver), while other events take a very long time even for a fast spacecraft, like flying to the Moon (1-5 days) or to Mars (3-7 months or more). Orbiter lets you speed up or slow down time to deal with these different time scales. Of course you are free to define whatever you consider to be important in terms of realism – if you think it’s better or more challenging to do everything in real time (1x), that’s OK – though you probably won’t be going very far from Earth at 1x time! You could even decide that speeding up time is OK, but slowing it down isn’t – again, it’s up to you, and you never have to slow down time to use Orbiter successfully. I just find it helpful sometime and wanted to let you know.
Questions About Other Stuff
I was wondering about the HUD and MFDs (multi-function displays) – what are they like in real life?
HUDs (head up displays) and MFDs (multifunction displays) started out in military aircraft, and HUDs are still most common in military aircraft where the pilot has many more things to worry about than even a commercial jet pilot (things like enemy aircraft and missiles), so keeping your “head up” and looking around is really critical. A few civilian aircraft (and the Space Shuttle) also use HUDs. MFDs are more common – they are used in virtually all modern military aircraft, nearly all civilian airliners, and even in some recent general aviation (small single/twin engine) airplanes.
HUDs make use of optical lenses and mirrors that are something like a computer video projector. But instead of projecting onto a white screen for viewing, the computer images are projected onto a semi- transparent “combiner” plate. It’s called a combiner because to the pilot, it combines the view of the outside world which is mostly far off (“at infinity”) with the imagery (numbers, lines, icons, etc. called “symbology”) generated by the flight computer. The optics are designed so that the symbology also appears to be projected “at infinity” so everything (real world and symbology) is in focus for the pilot.

MFDs are basically computer screens, most often LCD panels these days (they used to be CRT’s), built to work reliably under all flight conditions (various G-loads, high/low temperatures, etc.) and with special illumination systems to allow them to be clearly visible in all light conditions (strong sunlight is especially challenging). They typically have buttons around the edges of the screen that are labeled on-screen by the software according to the function in use (e.g., maps need buttons to zoom in/out). Some modern MFDs are also touch-sensitive (to allow direct designation of an airport or a target), and those in some military craft also can be operated by special buttons on the throttle and control stick (a system called HOTAS for hands-on throttle and stick). Leaning forward to press buttons on the MFD is not a big problem in an airliner, but in a fighter where the pilot may be experiencing 6G or more on a regular basis, it’s not as easy, and HOTAS is a very useful feature.
Wondering More
Of course Google.com and other search engines can help you find nearly anything, but here are a few more specific web sites you may find useful the next time you are just wondering about space stuff.
NASA has tons of information on everything related to space – dig around a little, and note that it’s sometimes easier to search NASA sites with Google.com by adding site:nasa.gov to your search string (this will search across all the many available NASA web sites) http://www.NASA.gov
Basics of Space Flight from JPL (JPL is part of NASA but is a very good starting point itself) http://www2.jpl.nasa.gov/basics/
European Space Agency (NASA is not the only agency with great web content) http://www.esa.int/esaCP/index.html
How Stuff Works (cool site for many topics, not just space, but this Hubble page is excellent) http://science.howstuffworks.com/hubble.htm http://science.howstuffworks.com/space-channel.htm (general space library, many topics)
Orbital Transfers between Planetary Orbits: An Example (a clever use of simple calculations) http://www.go.ednet.ns.ca/~larry/orbits/orbitrnf.html
Mars and Moon Website (personal web site of Dr. Donald Rapp, formerly of JPL) http://www.mars-lunar.net/
| Chapter 9: A Bit About Add-ons | GPIS Contents | Epilog: Your Future In Space |
Precis
This article has a precis and appears in the Random addon or Random article section on the Main Page. The precis can be found at GPIS 10: I Was Just Wondering/precis and is displayed below.
|
Go Play In Space, Chapter 10. Go Play In Space is the classic introduction to Orbiter for new orbinauts and those looking to expand their horizons. Chapter 10 addresses the age-old question: Is it safe to let the Wookie drive? They might not all be frequently asked, but many questions are answered here. (More...)
|